全连接神经网络长什么样
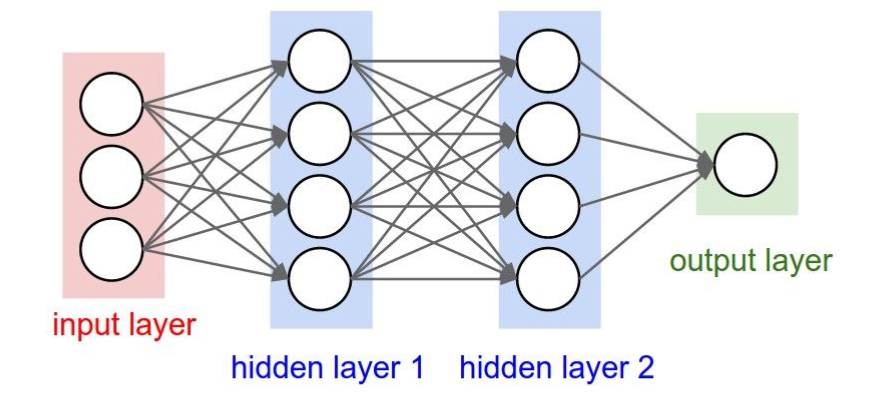
上图是一个双隐层的前馈全连接神经网络,或者叫多层感知机 (MLP)。它的每个隐层都是全连接层。它的每一个单元叫神经元。
如何实现一个简单的 FC 网络
从线性回归说起
给定由 d 个属性描述的实例 $x = (x_1; x_2; …; x_d)$,线性模型试图学习一个通过属性的线性组合来预测的函数,即 $$f(x) = \sum_{i=1}^d w_i x_i + b$$,写成向量表示即 $$f(x) = \mathbf{w^T} \mathbf{x} + b$$。那我们如何衡量$f(x)$与$y$之间的差别呢?在回归任务中,我们最常采用均方误差来度量,即$loss = \sum_{i=1}^n (f(x_i) - y)^2$。要使 loss 最小,我们可以分别对$w$和$b$求偏导数,令其为0,得到解析解:$$w = \frac{\sum_{i=1}^m y_i(x_i - \overline{x})}{\sum_{i=1}^m x_i^2 - \frac{1}{m} (\sum_{i=1}^m x_i)^2}$$
$$ b = \frac{1}{m} \sum_{i=1}^m (y_i - w x_i)^2$$
若$\mathbf{X^TX}$满秩,可写成向量形式:$$\mathbf{\hat{w}^*} = \mathbf{(X^T X)^{-1} X^T y}$$
感知机
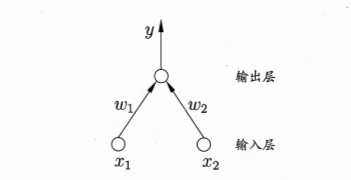
这是一个两输入神经元的感知机网络结构示意图,上文提到,单神经元感知机做了一个线性运算,再把结果输入激活函数,即 $y = f(\sum_{i=1}^n w_i x_i + b)$,f即为激活函数。但是单层感知机学习能力非常有限,无法解决线性不可分问题,如异或问题。这时我们就需要多层感知机。感知机隐层越多,理论上就能拟合越复杂的函数。
多层感知机 (Multilayer Perceptron, MLP)

我们说 MLP 是全连接神经网络,因为它的每一个神经元把前一层所有神经元的输出作为输入,其输出又会给下一层的每一个神经元作为输入,相邻层的每个神经元都有“连接权”。神经网络学到的东西,就蕴含在连接权和阈值(偏置)中。
由于引入了非线性的激活函数,感知机通常无法求得解析解,在深度神经网络中,损失函数通常是非凸的,所以只能求得数值解,而梯度下降法是最常用的方法。
反向传播 (Back Propagation, BP)
我们训练神经网络的目标,就是优化损失函数使其达到最小。不同的任务通常使用不同的损失函数。通常使用反向传播算法来训练神经网络。
下面以单隐层感知机为例,说明反向传播算法是如何工作的。假设每层神经元都用 Sigmoid 函数作为激活函数,并且使用均方误差函数作为损失函数。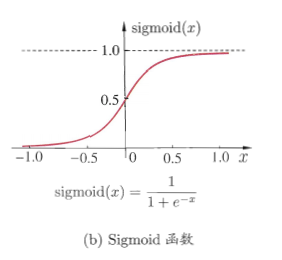
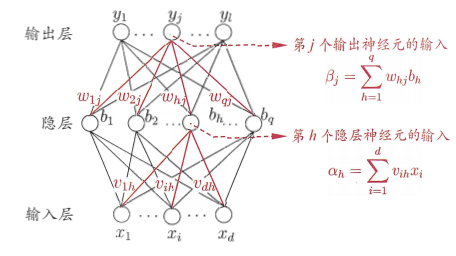
对训练例$(x_k, y_k)$,设神经网络输出为$\mathbf{\hat{y}_k} = (\hat{y}_1^k, \hat{y}_2^k, …, \hat{y}_l^k)$,即$$\hat{y}_j^k = f(\beta_j - \theta_j)$$
均方误差:$$E_k = \frac{1}{2} \sum_{j=1}^l (\hat{y}_j^k - y_j^k)^2$$
BP 是一个迭代学习算法,基于梯度下降策略,任意参数$v$的更新估计式为:$$v \leftarrow v + \Delta v$$
我们以$w_{hj}$进行推导,给定学习速率$\eta$,有:$$\Delta w_{hj} = -\eta \frac{\partial E_k}{\partial w_{hj}}$$
由链式规则:$$\frac{\partial E_k}{\partial w_{hj}} = \frac{\partial E_k}{\partial \hat{y}_j^k} \cdot \frac{\partial \hat{y}_j^k}{\partial \beta_j} \cdot \frac{\partial \beta_j}{\partial w_{hj}}$$
对于 Sigmoid 函数:$$f’(x) = f(x)(1 - f(x))$$
$$\begin{split}
g_j &= -\frac{\partial E_k}{\partial \hat{y}_j^k} \cdot \frac{\partial \hat{y}_j^k}{\partial \beta_j}\
&= -(\hat{y}_j^k - y_j^k)f’(\beta_j - \theta_j) \
&= \hat{y}_j^k (1 - \hat{y}_j^k)(y_j^k - \hat{y}_j^k)\end{split}$$
$$\Delta w_{hj} = \eta g_j b_h$$
对于其他参数,我们也采用一样的方法求得偏导数。但是上述过程比较复杂,实际上在神经网络模型中,我们采用计算图模型来实现自动求导。
计算图
以$f(w,x) = \frac{1}{1 + e^{-(w_0 x_0 + w_1 x_1 + w_2)}}$为例,演示计算图是怎么计算导数的。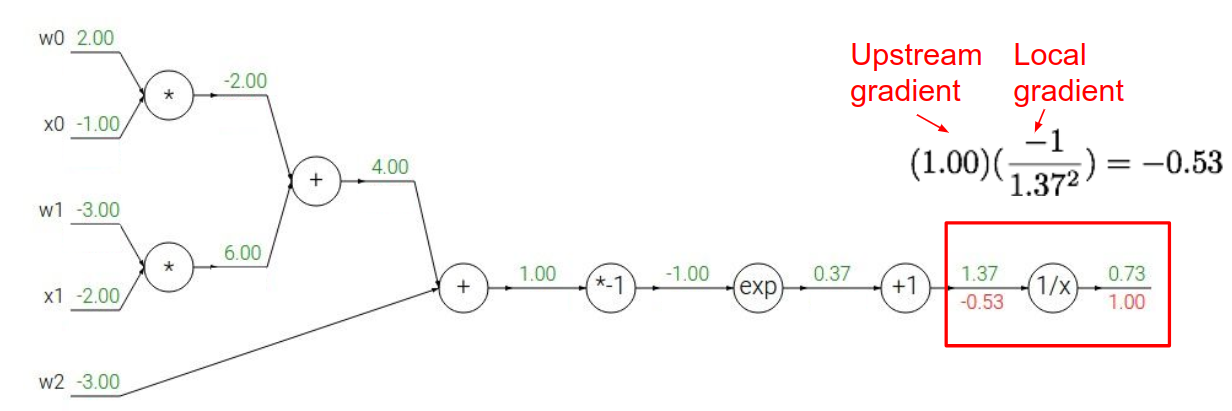
简单来说,要点就是链式规则。对一个节点n来说,它的输入为$x_n$,输出为$y_n$,损失函数为$L$,有$\frac{\partial L}{\partial x_n} = \frac{\partial L}{\partial y_n} \cdot \frac{\partial y_n}{\partial x_n}$,即 UpstreamGradient * LocalGradient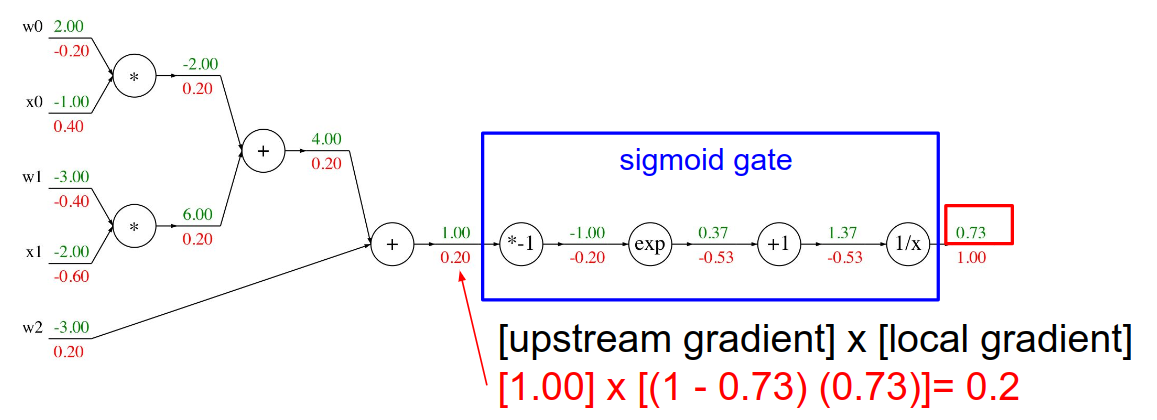
当然,我们可以把一个函数运算当做计算图的一个 Operation,即把函数运算涉及到的节点合并成一个节点。如 Sigmoid 的导数:$\sigma’(x) = \sigma(x) (1 - \sigma(x))$,计算过程如上图。
全连接层有什么用
全连接的核心操作是矩阵乘法,本质上是把一个特征空间线性变换到另一个特征空间。实践中通常是把特征工程(或神经网络)提取到的特征空间映射到样本标记空间,参数$\mathbf{w}$相当于做了特征加权。
由于这个特性,在 CNN 中,FC 常用作分类器,即在卷积、池化层后加 FC 把特征变换到样本空间。而卷积可以看做一定条件约束的“全连接”,如用 1 * 1 的卷积,可以与全连接达到同样的效果。
但是由于全连接层参数冗余,有些模型使用全局平均池化 (Global Average Pooling, GAP) 来代替全连接。
不过在迁移学习中, FC 可充当“防火墙”,不含 FC 的网络微调后效果比含 FC 的差。特别在目标域和源域差别比较大的,FC 可保证模型表示能力的迁移。
FC 的应用
- Ubisoft 使用 FC 来迁移人物运动模型参数。
- MNIST 手写数字识别
- 配合强化学习来训练游戏机器人
- 数据库索引
- 排序算法
- 优化缓存系统
- 预测太阳耀斑
- 碰撞实时预警